É A HORA E VEZ DE 2017

Clique no centro do vídeo para ler e ouvir a mensagem.

UM FELIZ 2017 PARA TODOS

É NATAL!

Chega dezembro e com ele vem o Natal. No ar há uma atmosfera que envolve a todos. As lojas, ruas e casas se enfeitam para a grande festa.

E o povo se anima à medida que o Natal se aproxima. A correria é grande. Lojas apinhadas de gente que tem um único intuito: encontrar o presente ideal para cada familiar ou amigo. Depois, o mesmo acontece para escolher os quitutes da ceia. 

E chega o dia da festa. Num canto da sala, sob a árvore enfeitada, algumas caixas com presentes. Dentro delas, um mimo aguardado que trará a felicidade e a alegria de quem oferta e de quem recebe.

Que neste NATAL possamos encontrar em cada caixa: muito amor, respeito, solidariedade e paz.

FELIZ NATAL!

PARALISIA CEREBRAL E A MATEMÁTICA (II)

Na postagem anterior, vimos que a paralisia cerebral pode impedir os movimentos, mas não impede a criança ou jovem de aprender, mesmo que seja, aquilo que é básico, ou o mínimo como se costuma dizer. O importante é que essa criança ou jovem tenha a oportunidade de aprender de acordo com suas possibilidades.

Paramos na apresentação da segunda série numérica, ou seja, do 20 ao 29. Dessa forma, apresento a mesma série, com o objetivo de retomar o assunto e fixá-la na memória. 

Após a leitura dos numerais de 20 a 29, lembro que 2 saquinhos de tampinha formam o 20. E sigo acrescentando uma unidade até que se completem 29, para que ele tenha noção da quantidade que acabou de ler. Em seguida, começamos os exercícios no caderno.

VIZINHOS DO NÚMERO 

Neste exercício, uniremos dois exercícios já feitos anteriormente: encontrar o que vem “antes” e o que vem “depois”, mas em um só exercício. Antes converso com ele sobre os vizinhos de sua casa e objetos que estão próximos a nós, como forma de tornar a teoria o mais concreto possível. Entendido o termo “vizinho”, vamos ao exercício. Como é novidade para ele, permite que se oriente olhando a série que está sendo estudada. 

E espalhando os numerais sobre a mesa, ele escolhe apontando os números e depois cola-os no lugar correto.

NOÇÃO DE NÚMERO MAIOR

Preparando o assunto que vem a seguir, trabalho com ele o número maior e para que entenda, voltamos com as tampinhas. Mostro duas quantidades quaisquer e pergunto: Qual delas tem mais tampinhas? E ele aponta. Pergunto por que ele escolheu aquela quantidade? E ele responde: porque tem mais. Elogio e digo: Quem tem mais é “maior”. Pergunto novamente: E quem tem menos? Ele aponta e diz: Quem tem menos é menor. Elogio seu raciocínio.

Mostro o exercício e peço que faça uma marca no maior.

E depois de marcado elogio novamente.

ORDEM CRESCENTE

O primeiro passo é fazê-lo entender o que quero. Mostro a ele uma torre de poucas peças. Ela tem a forma quadrada. E peço que ele a monte. Em quanto isso, pergunto se quando ele era bem pequeno, bebê ainda, se ele tinha o tamanho que tem hoje?

Ele riu e disse que não, que ele era pequeno. Insisto e pergunto: E por que você está do tamanho que tem hoje? Ele ri novamente e responde: - porque eu cresci. Estava aí, a palavra que eu queria ouvir.

Retomo então a questão: Então, começamos pequenos e terminamos grandes. E peço que arrume sobre a mesa, começando do pequeno para o grande.

Depois de pronta, digo: quando colocamos os objetos numa ordem que vai do pequeno para o grande, como você fez aqui, dizemos que essa arrumação está em “ORDEM CRESCENTE”, porque cada peça fica um pouco maior do que a que vem antes dela. Então, vai do pequeno para o grande.Como segundo passo, colar peças na ordem crescente.

  

O resultado final foi este:

Feito isso, mostro alguns numerais, todos fora de ordem e digo a ele que se podemos colocar objetos na ordem crescente, também podemos colocar os numerais. E peço que ele cole os numerais também na ordem crescente. E vejam como ele fez direitinho.

Aguardem novas postagens sobre o assunto.

PARALISIA CEREBRAL E A APRENDIZAGEM MATEMÁTICA

Olá pessoal, mais uma vez venho trazer sugestões no ensino e registro da aprendizagem das noções matemáticas. O garoto em questão tem Paralisia Cerebral de moderada a grave, é cadeirante, tem como comorbidades a deficiência intelectual, baixa visão e problemas motores espásticos, onde apenas a mão direita é ativa e mesmo assim, apresenta dificuldades nos movimentos. 

Para fixar a numeração, a sugestão é um desenho com alguma dificuldade, como este por exemplo:

A dificuldade maior está na no ziguezague dos pelos do gato. Minha intensão ao escolher este desenho é verificar se ele consegue cobrir o pontilhado. o resultado foi o seguinte: o ziguezague na parte inicial ele foi muito bem, porém, o do alto da cabeça ele seguiu reto e não fez o ziguezague porque teve um espasmo bem nesse momento.

Na postagem anterior, terminei mostrando a série de 10 a 15. Como completava a série que ele afirmava não saber e para verificar se houve memorização da forma e da nomenclatura, é por ela que começo, com a leitura da série já aprendida. E antes de ensinar o restante, verifico o "antes" de alguns números dados.

No alto da página, a sequência trabalhada que serve para a leitura dos números e fonte de pesquisa durante os exercícios.

Em seguida, o "depois" de outros números da série ou família numérica do 10.

A resposta possível, neste momento, ainda é a colagem. Por causa dos espasmos que aparecem sempre que se esforça um pouco. Em seus registros os números ficam irreconhecíveis. mas estamos trabalhando a coordenação motora fina, mas suas melhoras serão mais lentas. O mesmo exercício e com o mesmo procedimento foi feito com o restante da série (15 a 19)

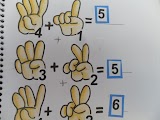
Procurando novas oportunidades de contagem e de registros, decidi ensiná-lo a contar os dedos ao realizar as adições.

Mas, não deu certo. Ele não conseguia manter os dedos indicados em pé, por causa do problema motor e dos espasmos. Mas, como é muito esperto, ele arranjou uma estratégia: contar os dedinhos do desenho. Mas, fica a dica para os que conseguem.

NOÇÃO DE VINTE

Terminado este exercício, lembrei-o das 10 tampinhas que contara e colocara no saquinho semanas atrás. 

 

Perguntei quantas tampinhas havia no saquinho e sem titubear respondeu serem 10. Coloco então o numeral correspondente. A partir de então, coloco uma a uma as tampinhas até completar 9. E a cada tampinha colocada eu perguntava: 10 mais 1 fica? E ele respondia acertadamente. E seguida, coloco mais uma (formando 10  unidades) e ele novamente as pôs num outro saquinho.

Apresento o novo número (20) e digo a ele que começará uma nova serie, agora com o 2 na frente, porque ele representa os 2 saquinhos com 10 tampinhas cada um.

 

Terminado e entendido, voltamos ao caderno. Lá, retomo a explicação e apresento a série.

E fazemos a leitura desses numerais. E para finalizar, um Liga-Pontos com a nova série.

Vejam como ele ia ligando os pontinhos corretamente.

A curvatura no percurso é devido a um espasmo que 

ele não consegue controlar. 

Os leitores que me acompanham desde o início do blog, sabem que gosto de trabalhar com o Material Dourado. No entanto, devem estar se perguntando por que estou usando tampinhas? Nesta etapa e com este garoto, estou usando as tampinhas porque os cubinhos são muito pequenos e devido aos espasmos ele os derruba e também porque não é tão fácil de manejá-los, devido a baixa visão. Com as tampinhas, por serem maiores, fica melhor.

Espero que estas sugestões sejam do seu agrado.

Continuamos com mais dicas

OS REGISTROS POSSÍVEIS EM MATEMÁTICA

É comum pais e professores acreditarem que crianças e adolescentes com Paralisia Cerebral e sérios problemas motores não consigam aprender os conteúdos escolares. Por essa razão, esses estudantes passam horas sem fazer nada. Essa crença é mito e todos podem aprender respeitando-se sua forma de aprender e suas limitações.  

A primeira coisa que precisamos saber é esse aluno sabe e se consegue “CONTAR”. E se não souber, temos aqui o ponto de partida. O garoto que atendo, afirmava que só sabia contar e reconhecer os números até 10.  E para verificar a veracidade dessa informação, coloquei grupos diferentes de quantidades para que contasse, identificasse os numerais e os colasse a resposta no lugar indicado em cada grupo.

Diante da certeza de que ele conseguia contar, parti para novos conhecimentos. O conhecimento do “onze”.

Primeiro, fiz com que contasse 10 tampinhas de refrigerante e colocá-las num saco plástico pequeno. E para que visualizasse a quantidade simbolicamente escrevi o numeral correspondente. Montei e desmontei várias vezes. Só então, coloquei mais uma tampinho e falei o nome “ONZE”.  

Coloquei outra e ele falou “DOZE”. E fomos fazendo assim até o “QUINZE”. Ele mostrou que sabia mais do que havia falado. Então, passamos para o caderno.

 

Feito isso, verifiquei se ele conseguia juntar os conjuntos apresentados e reconhecer os numerais. Bastou olhar para ir contando  e disse ao terminar: Dá 6. Elogiei-o por isso. Espalhei os numerais sobre o caderno e pedi que mostrasse qual era o “6”. Ele apontou corretamente. Peguei o cartão escrito com o 6, passei cola, e entreguei a ele para que colasse no lugar correto. E ele fez direitinho.

 

No atendimento seguinte, revimos o 10 e o 11 e partimos para quantidade maiores: 12, 13, 14 e 15. Sempre procedendo da mesma maneira.

Ele contou, apontou o numeral e procedemos a colagem dos numerais. 

 FAZENDO CONTAS

Na folha seguinte mais algumas continhas de adição com quantidades maiores (do 9 a 15). 

 

NOÇÃO DE ANTES E DEPOIS

Aproveitei os numerais para trabalhar essas noções, usando os numerais de 10 a 15 que foram trabalhados. Fizemos isso usando o reconhecimento dos numerais e da colagem (os que tem a borda mais escura para destacar o trabalho dele).

 

Aproveitei a oportunidade para trabalhar essa noção para completar as séries a) de 1 a 10 e b) de 10 a 15, colocando um tracinho indicando os que estavam faltando, do mesmo jeito como fazemos na lousa. 

 

Ele percebeu o número faltante, reconheceu os números colocados sobre o caderno, e colou-os no caderno como se vê na foto.

Espero que aproveitem estas ideias. Continuamos com 

mais ideias na próxima postagem.

MAIS FORMAS DE REGISTRO POSSÍVEIS

Muitas vezes, os problemas motores causam problemas para a escrita convencional e, muitas vezes, tornando-a impossível. Não há necessidade de pressa ou ficar angustiado porque a criança com PC não consegue escrever da maneira convencional.

E independente de nossas crenças, conceitos e preconceitos a respeito da Paralisia Cerebral, é preciso tentar alguma coisa, visto que pessoas nessas condições tem sonhos e desejo de aprender.

À medida em que trabalhamos com alunos com Paralisia Cerebral vamos percebendo as possibilidades que eles apresentam. E, se não podem escrever, podem fazer alguma outra coisa.

LIGAR é uma alternativa, como vimos anteriormente. Porém se usarmos apenas esta alternativa para tudo, se tornará monótona e passamos para essa criança que ela só pode fazer isso. Por isso, é preciso experimentar novas formas. Se der certo, ótimo. Se não der, procuramos outras para alternar nas atividades.

Uma outra forma é “CIRCULAR” figuras, palavras, sílabas, letras e números. Eu tentei com o garoto que atendo, mas não deu certo. Por isso, peço que faça uma “MARCA” que saiba fazer. Essa “marca” pode ser um risco, uma tentativa de círculo, um quadrado, um (X) ou outra coisa qualquer.

Se a Paralisia Cerebral for “espástica” os movimentos são descoordenados e quando inicia um movimento, a “espasticidade” faz com que os traços desviem da rota e fiquem sem rumo e trêmulas. Por mais que a criança insista em voltar para o movimento iniciado, não conseguem dominar os movimentos. É preciso que se entenda que cada criança com Paralisia Cerebral, ou outra dentre as inúmeras “síndromes” existentes, apresentam possibilidades diferentes devido ao tipo de comorbidade que apresentam e a (s) área (a) que envolvem.

Se a criança não pode escrever, como a maioria das crianças, podem “MONTAGEM DE PALAVRAS” com o alfabeto móvel ou com materiais alternativos. Este tipo é bom porque podemos trabalhar a sequência de letras existentes numa palavra ou sílaba. Podemos trabalhar também a leitura das palavras formadas, mesmo que a leitura seja lenta e pensada do tipo B + A = BA. 

 

 

Usando essa forma de escrita, podemos ainda trabalhar o número de letras e sílabas que a palavra formada tem. Podemos ainda trabalhar a separação e a junção de sílabas, incluindo a leitura.

Com as sílabas aprendidas podemos formar pequenos cartões que servem para formar novas palavras. 

Se a criança colocar letras que formam palavras sem sentido ou sem significado, nos dá a chance de explicarmos o porquê isso não deve ser feito. Exercícios como este facilita a visualização a diferença na quantidade de letras que as sílabas podem ter. E se não perceberem sozinhos, podemos chamar a atenção da criança para elas.

Com esse material, podemos mostrar como fica a separação de sílabas. Se não conseguem perceber sozinhos, podemos chamar a atenção para a observação das letras existentes em cada pedaço.

Com o mesmo material podemos trabalhar as sílabas iniciais de palavras, para que compreendam de modo concreto que outras palavras podem começar com a mesma sílaba. O mesmo pode acontecer com palavras que terminam com a mesma sílaba.

Mas podemos avançar e tornar mais dinâmica o aprendizado. Com uma “COLAGEM” podemos trabalhar vários exercícios que passamos no quadro para a maioria das crianças, como completar palavras com letras ou sílabas e completar frases com palavras inteiras.

Vejam:

 

1- Nomeando figuras

 

2- Ler a palavra e encontrar a figura 

correspondente e colar no lugar correto.

 

3- Completando as palavras com as

 sílabas que faltam.

 

 

4- Completando frases com palavras sugeridas 

por desenho ou figura.

Como registrar as questões matemáticas?

Aguardem a próxima postagem